🗓️ May 2024👀 loading

Deriving the Mortgage Payment Formula

Presenting how the formula for monthly mortgage payments is mathematically derived from the definition of an annuity loan.

financemortgagepaymentexcelmath

I'll show you how to derive the mortgage formula for monthly payments:

A = P\frac{\frac{R}{12}(1 + \frac{R}{12})^n}{(1 + \frac{R}{12})^n - 1}

where

\begin{aligned} A &= \text{the monthly payment amount}\\ P &= \text{the mortgage principal}\\ R &= \text{the fixed annual interest rate}\\ n &= \text{the mortgage duration, in months}\\ \end{aligned}

For example, for a 30 year $500,000 mortgage, with a fixed annual interest rate of 6%, we'd have:

\begin{aligned} A &= P\frac{\frac{R}{12}(1 + \frac{R}{12})^n}{(1 + \frac{R}{12})^n - 1}\\ &= 500,000 \cdot \frac{\frac{0.06}{12}(1 + \frac{0.06}{12})^{360}}{(1 + \frac{0.06}{12})^{360} - 1}\\ &\approx 2997.75\\ \end{aligned}

Which means that the described mortgage incurs monthly payments of $2,997.75.

This number corresponds with Microsoft Excel's built-in PMT function.

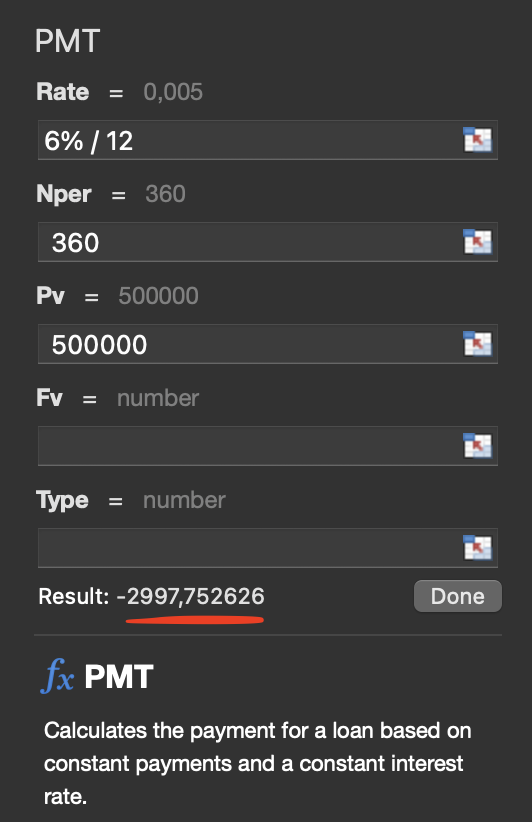
microsoft excel's PMT payment function yielding a result of -2997,752626 for the parameters Rate equal to 6% / 12, Nper equal to 360, and Pv equal to 500.000

So let's see where this formula comes from.

Annuity Loan Characteristics
Principal Payment Formula
- Proposal for a Non-recursive Identity
- Proof for the Non-recursive Identity
Annuity Payment Formula
- Monthly vs. Annual Interest Rates

Annuity Loan Characteristics

We'll be looking at so-called annuity loans, which are characterised by the following properties:

The loan starts out by lending a certain amount of money, denoted $P$ for principal amount
The lender is expected to pay back this loan in a fixed number of $n$ equal payments, for some natural number $n > 0$
Such payments are called annuities, where the annuity amount, denoted $A$ $A$ , remains constant throughout the loan, and always consists of two components:
- interest
- principal repayment
The interest component varies month-to-month, because it's calulated by multiplying an agreed-upon fixed interest rate $r$ (greater than zero) with the remaining principal (i.e. the original principal amount $P$ minus all previous principal repayments)
The principal repayment varies month-to-month as well, in such a way that the annuity $A$ remains constant for the entire loan duration

After making $n$ annuity payments of exactly $A$ dollars (euro's, pounds, whatever), your loan will be completely paid off. Put differently: the principal repayment component of each of those $n$ annuities will add up to your original principal amount $P$ .

Below you'll find a typical loan repayment diagram with 12 annuities, showing how the monthly annuity $A$ remains constant from start to finish.

12 vertical bars of the same height of A units, where each bar contains the colors blue (for principal repayment) and pink (for interest), where the blue part makes up for about 10% in the first bar, and steadily increases until it makes up for about 95% in the twelfth bar

The sum of all blue bars is equal to $P$ .

This diagram also shows that the total amount of interest can easily surpass the principal payment amount $P$ , depending on the interest rate $r$ .

Take our 30 year mortgage from the introduction, for example. We calculated that a $500,000 principal at an annual interest rate of 6% corresponds to a monthly annuity of $2,997.75. So when you've paid off your mortgage after making 360 of these $2,997.75 payments, you would've paid the bank a grand total of $1,079,190, consisting of the $500,000 principal and $579,190 of interest.

It's good to be a bank 🙂

Principal Payment Formula

The main goal of this article, is to find a formula for the monthly annuity amount $A$ .

In preparation, we'll start by studying the following sequence

(P_k)_{k=0}^n = (P_0, P_1, P_2, P_3, \dots, P_n)

with $P_k$ defined as the remaining principal after making $k$ annuity payments.

From this, it immediately follows that $P_0 = P$ .

But what is $P_1$ ? In other words: how much do we owe the bank after making our first annuity payment?

Well, since the annuity amount $A$ remains constant throughout the loan's entire duration, this first payment has reduced our loan principal by some amount less than $A$ :

the interest component of this first payment is equal to $r \cdot P$
the remaining part of $A$ is principal reduction, i.e.: $A - r \cdot P$

In other words:

\begin{aligned} P_1 &= P - (A - rP)\\ &= P_0 - (A - rP_0) \end{aligned}

We can capture this notion in a more general sense.

The remaining principal $P_{k+1}$ after making a total of $k+1$ annuity payments is equal to the previous remaining principal $P_k$ minus the principal repayment component of the $(k+1)$ -th annuity:

\begin{aligned} P_{k+1} &= P_k - (A - rP_k)\\ &= P_k(1 + r) - A \end{aligned}

This recursive identity for $P_{k+1}$ in terms of $P_k$ will eventually give us a formula for $A$ .

Proposal for a Non-recursive Identity

So, how can we turn this recursive identity $P_{k+1} = P_k(1 + r) - A$ into a single, non-recursive formula for $P_k$ ?

It usually helps to write out the first few terms, to see if a pattern can be detected.

\begin{aligned} P_0 &= P\\[10pt] P_1 &= P_0(1 + r) - A\\ &= P(1 + r) - A\\[10pt] P_2 &= P_1(1 + r) - A\\ &= \bigl(P(1 + r) - A\bigr)(1 + r) - A\\ &= P(1 + r)^2 - A(1 + r) - A\\[10pt] P_3 &= P_2(1 + r) - A\\ &= \Bigl(P(1 + r)^2 - A(1 + r) - A\Bigr)(1 + r) - A\\ &= P(1 + r)^3 - A(1 + r)^2 - A(1 + r) - A \end{aligned}

From this, it seems like the following pattern is beginning to emerge:

P_{k+1} = P(1 + r)^{k+1} - A\sum_{j=0}^{k}(1 + r)^j

Please note that this formula is just a guess at this point. We'd have to actually prove that this formula satisfies the recursive identity from the previous chapter.

But if the formula above were correct, that would be great, because we recognise the last term in this expression as the geometric sum:

\sum_{j=0}^k x^j = \frac{1 - x^{k + 1}}{1 - x}\\

for any $x \neq 1$ .

So we can let $x = (1 + r)$ because $r$ was assumed to be greater than zero, and reformulate our proposal for the $P_{k+1}$ formula.

\begin{aligned} P_{k+1} &= P(1 + r)^{k+1} - A\sum_{j=0}^{k}(1 + r)^j\\ &= P(1 + r)^{k+1} - A\frac{1 - (1 + r)^{k + 1}}{1 - (1 + r)}\\ &= P(1 + r)^{k+1} - \frac{A}{r}\Bigl((1 + r)^{k + 1} - 1\Bigr) \end{aligned}

Now, as a special case, note what happens if we let $k + 1 = 0$ :

\begin{aligned} P_0 &= P(1 + r)^0 - \frac{A}{r}\Bigl((1+r)^0 - 1\Bigr)\\ &= P - \frac{A}{r}(1 - 1)\\ &= P \end{aligned}

This suggests that we can actually put forward a single proposal for the $P_k$ formula, which should allow us to calculate the remaining principal after making $k$ annuity payments, for any $k$ with $0 \leq k \leq n$ :

P_k = P(1 + r)^k - \frac{A}{r}\Bigl((1 + r)^k - 1\Bigr)

Proof for the Non-recursive Identity

We set out to find a simple formula for $P_k$ which would satisfy the following recursive identity:

P_{k+1} = P_k(1 + r) - A

Then, in the previous section, we put forward the following proposal:

P_k = P(1 + r)^k - \frac{A}{r}\Bigl((1 + r)^k - 1\Bigr)

But we still need to prove that our proposal indeed satisfies the recursive identity. We'll do so by checking whether the expression $P_k(1 + r) - A$ indeed equals $P_{k+1}$ .

Here we go:

\begin{aligned} P_k(1 + r) - A &= \Biggl(P(1 + r)^k - \frac{A}{r}\Bigl((1 + r)^k - 1\Bigr)\Biggr)(1 + r) - A\\ &= P(1 + r)^{k + 1} - \frac{A}{r}\Bigl((1 + r)^{k + 1} - (1 + r)\Bigr) - A\\ &= P(1 + r)^{k + 1} - \frac{A}{r}\Bigl((1 + r)^{k + 1} - 1\Bigr) + \frac{A}{r}r - A\\ &= P(1 + r)^{k + 1} - \frac{A}{r}\Bigl((1 + r)^{k + 1} - 1\Bigr)\\ &= P_{k + 1}\\ \end{aligned}

This concludes the proof that our proposal for $P_k$ is indeed correct.

Annuity Payment Formula

We've proven our formula for the remaining principal after making $k$ annuity payments:

P_k = P(1 + r)^k - \frac{A}{r}\Bigl((1 + r)^k - 1)\Bigr)

Let's rephrase this equation to find an expression for $A$ :

A = r\frac{P(1 + r)^k - P_k}{(1 + r)^k - 1}

Now, even though the symbol $k$ appears in the formula for $A$ , we know that it's actually independent of $k$ . Because it doesn't matter how many payments you've made, the annuity remains constant from start to finish. As noted before, this is a defining characteristic of annuity loans.

This means that if we knew of a particular $k$ and its corresponding $P_k$ value, we could simply plug those into the formula above, and simplify the expression in such a way that the symbol $k$ no longer occurs.

One such $k$ is $k = 0$ , corresponding to $P_0 = P$ . But we've already used this fact when defining the recursive relation for $P_{k+1}$ in terms of $P_k$ . Attempting to use this fact for a second time doesn't yield anything useful:

\begin{aligned} A &= r\frac{P(1 + r)^0 - P_0}{(1 + r)^0 - 1}\\[15pt] &= r\frac{P - P}{1 - 1}\\[15pt] &= \:??? \end{aligned}

But there's another $k$ we can use!

Remember how one of the characteristics of an annuity loan, is that it's completely paid off after making $n$ payments. This implies that $k = n$ corresponds with $P_n = 0$ .

Plugging these values into our formula for $A$ yields the following result:

\begin{aligned} A &= r\frac{P(1 + r)^n - P_n}{(1 + r)^n - 1}\\[15pt] &= P\frac{r(1 + r)^n}{(1 + r)^n - 1} \end{aligned}

where

\begin{aligned} A &= \text{the recurring annuity payment amount}\\ P &= \text{the loan principal}\\ r &= \text{the loan interest rate}\\ n &= \text{the number of payments required to pay off the loan}\\ \end{aligned}

Monthly vs. Annual Interest Rates

Let's take a moment to dive into a little detail of the formula we have just derived:

A = P\frac{r(1 + r)^n}{(1 + r)^n - 1}

But what are $r$ and $n$ , and how are they "linked" exactly?

The number $n$ refers to the total number of payments you'll be making during the loan's duration
The number $r$ refers to the interest rate that's being multiplied with the total remaining principal, in order to determine the interest component for the upcoming payment

For example, in case of a 30 year mortgage, you'll be tempted to set $n = 30$ , but that would only be true when paying your mortgage once per year, rather than monthly.

Under normal circumstances, you'd set $n = 360$ , corresponding with the number of monthly mortgage payments.

As for the interest variable, you'll be tempted to set $r = 0.06$ in case of a mortgage with a fixed 6% annual interest and 360 monthly payments, but that would only be true if 6% were the monthly interest rate, rather than the annual interest.

An annual interest rate of 6% means that you're expacted to pay the bank 6% of the remaining principal, once per year.

a big blue bar labeled "remaining principal" on the left, separated by a vertical dashed line from a one-year timeline containing the months January through Februari, with a big "6%" label in the middle, and an arrow pointing from the "6%" label towards the big blue bar on the left

And so this 6% doesn't really apply to a typical mortgage with monthly payments.

In order to apply our 6% annual interest rate to a monthly payment schedule, we must somehow spread this single annual interest payment over 12 separate months.

This is done by dividing the annual interest rate by 12 in order to convert it into a monthly interest rate.

a big blue bar labeled "remaining principal" on the left, separated by a vertical dashed line from a one-year timeline containing the months January through Februari, with twelve blue vertical bars decreasing in size, with each of these twelve bars containing a "6% / 12" label and an arrow pointing to the previous blue bar on the left

This brings us to the final formula of this article, which can be used for determining the monthly payment amount for a mortgage with a fixed interest rate.

A = P\frac{\frac{R}{12}(1 + \frac{R}{12})^n}{(1 + \frac{R}{12})^n - 1}

where

\begin{aligned} A &= \text{the monthly payment amount}\\ P &= \text{the mortgage principal}\\ R &= \text{the fixed annual interest rate}\\ n &= \text{the mortgage duration, in months}\\ \end{aligned}

Deriving the Mortgage Payment Formula

Table of Contents

Annuity Loan Characteristics

Principal Payment Formula

Proposal for a Non-recursive Identity

Proof for the Non-recursive Identity

Annuity Payment Formula

Monthly vs. Annual Interest Rates